Robust Sparse Mean Estimation via Incremental Learning

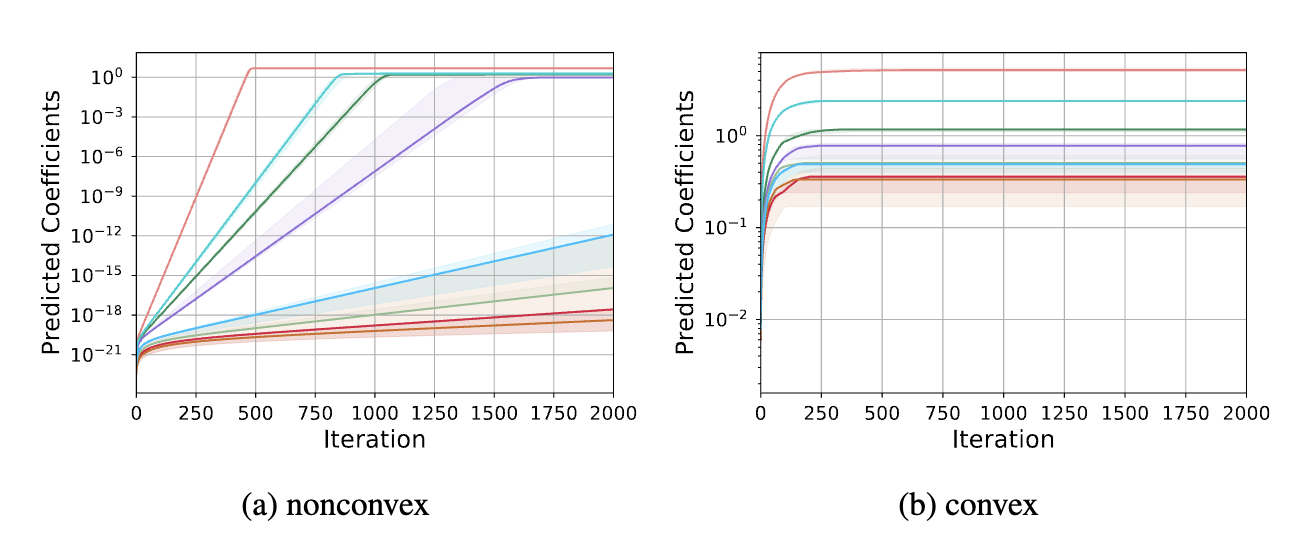
In this paper, we study the problem of robust sparse mean estimation, where the goal is to estimate a \(k\)-sparse mean from a collection of partially corrupted samples drawn from a heavy-tailed distribution. Existing estimators face two critical challenges in this setting. First, they are limited by a conjectured computational-statistical tradeoff, implying that any computationally efficient algorithm needs \(\tilde{\Omega}(k^2)\) samples, while its statistically-optimal counterpart only requires \(\tilde{O}(k)\) samples. Second, the existing estimators fall short of practical use as they scale poorly with the ambient dimension. This paper presents a simple mean estimator that overcomes both challenges under moderate conditions: it runs in near-linear time and memory (both with respect to the ambient dimension) while requiring only \(\tilde{O}(k)\) samples to recover the true mean. At the core of our method lies an incremental learning phenomenon: we introduce a simple nonconvex framework that can incrementally learn the top-\(k\) nonzero elements of the mean while keeping the zero elements arbitrarily small. Unlike existing estimators, our method does not need any prior knowledge of the sparsity level \(k\). We prove the optimality of our estimator by providing a matching information-theoretic lower bound. Finally, we conduct a series of simulations to corroborate our theoretical findings.